On the cover: Spiderman: Far from home, London bridge fight scene
Remember that crazy London bridge fight scene in the movie Spiderman: Far From Home, where a drone swarm kicks Tom Holland’s ass? Ever wondered how all those drones could work together in such harmony while not colliding with each other? Enter Optimal Reciprocal Collision Avoidance (ORCA) and formation flights.
The basic requirement for an intelligent drone swarm is collision avoidance. Once collision avoidance is achieved, the drones can be made to follow an arbitrary formation similar to bird flocking.
Collision avoidance (commonly referred as Obstacle avoidance) is a standard problem in robotics. In a static environment with stationary obstacles, collision avoidance is achieved by path planning algorithms such as Dijkstra and A*. But a dynamic environment with moving obstacles requires both path planning and real time velocity planning (you never know who’s gonna come at you anytime). There are many algorithms that have been developed over the years for this problem like Visibility Graph Algorithm (VGA), Timed Elastic Band (TEB) and Dynamic Window Approach (DWA).
But all of these algorithms work in the assumption that anything outside of the robot itself is an obstacle, even other robots (talk about narcissistic robots). What happens when it’s a swarm of intelligent robots where each of them are looking to avoid collision simultaneously? There must be a better solution right? Are you thinking, hey perhaps the robots that are about to collide with each other can share the responsibility of avoiding collision? Yes, you are right and it can be done! This is called reciprocal collision avoidance.
In this post I will talk about a concept called Velocity Obstacle based on which reciprocal collision avoidance algorithms are built. What the hell is a “velocity obstacle” you ask? Well, brace yourselves :)
NOTE: Velocity Obstacle is not the only method for reciprocal collision avoidance. There are other algorithms for this such as Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) and others similar to these with modifications according to the type of system (AGVs/UAVs/AUVs).
Let’s take two circular robots A and B with radii of $r_A$ and $r_B$, at positions $p_A$ and $p_B$, moving with velocities $v_A$ and $v_B$ respectively like below:
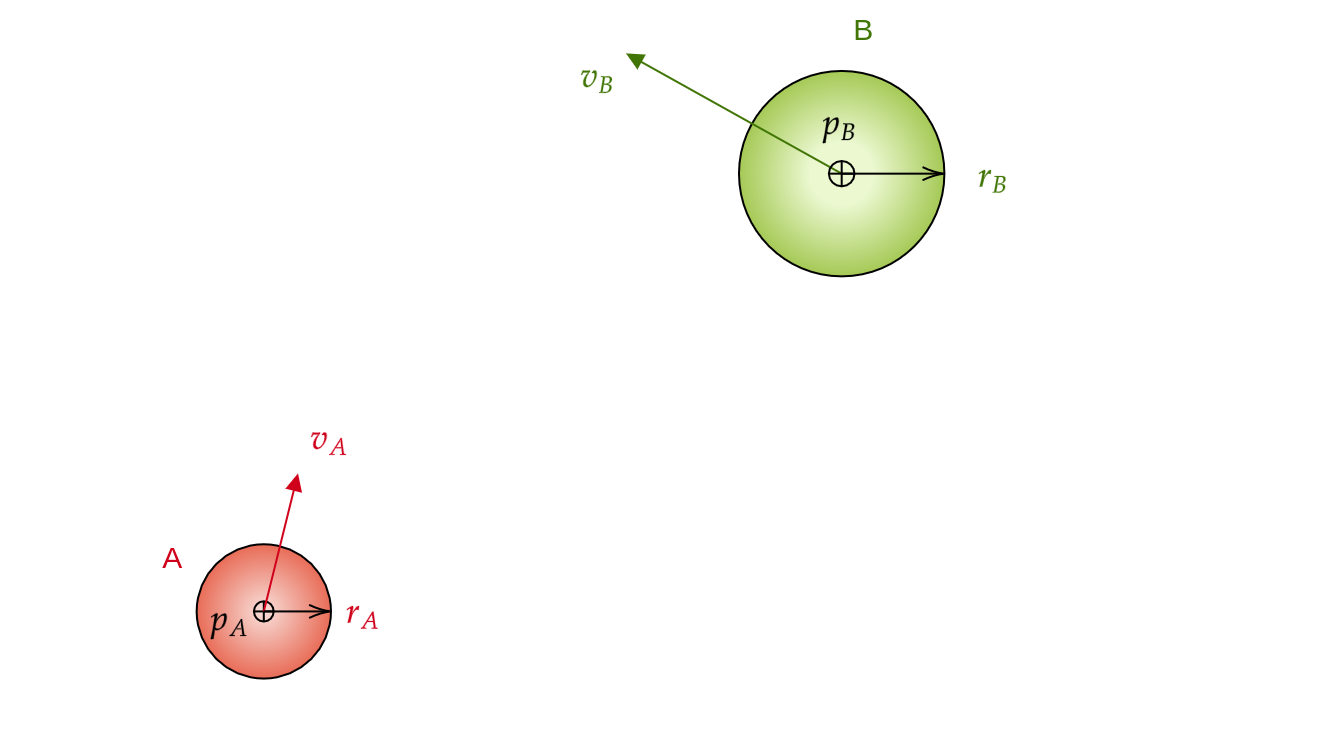Figure 1: Two robots A and B in the environment; setting the scene
For the sake of simplicity, we will restrict ourselves to 2D plane and circular robots. Now, let’s make the robot A’s radius to zero, ie., reduce it to a point and inflate the radius of agent B by the radius of A ie., $r_A + r_B$. Let’s also calculate the relative velocity of robot A wrt to B: $\mathbf{v_{AB}} = \mathbf{v_A} - \mathbf{v_B}$. This is the velocity with which robot A is moving towards robot B. For ease of derivation we will also translate the origin to the position of robot A. So now, the robot A is at the new origin and robot B is at $p_B - p_A$.
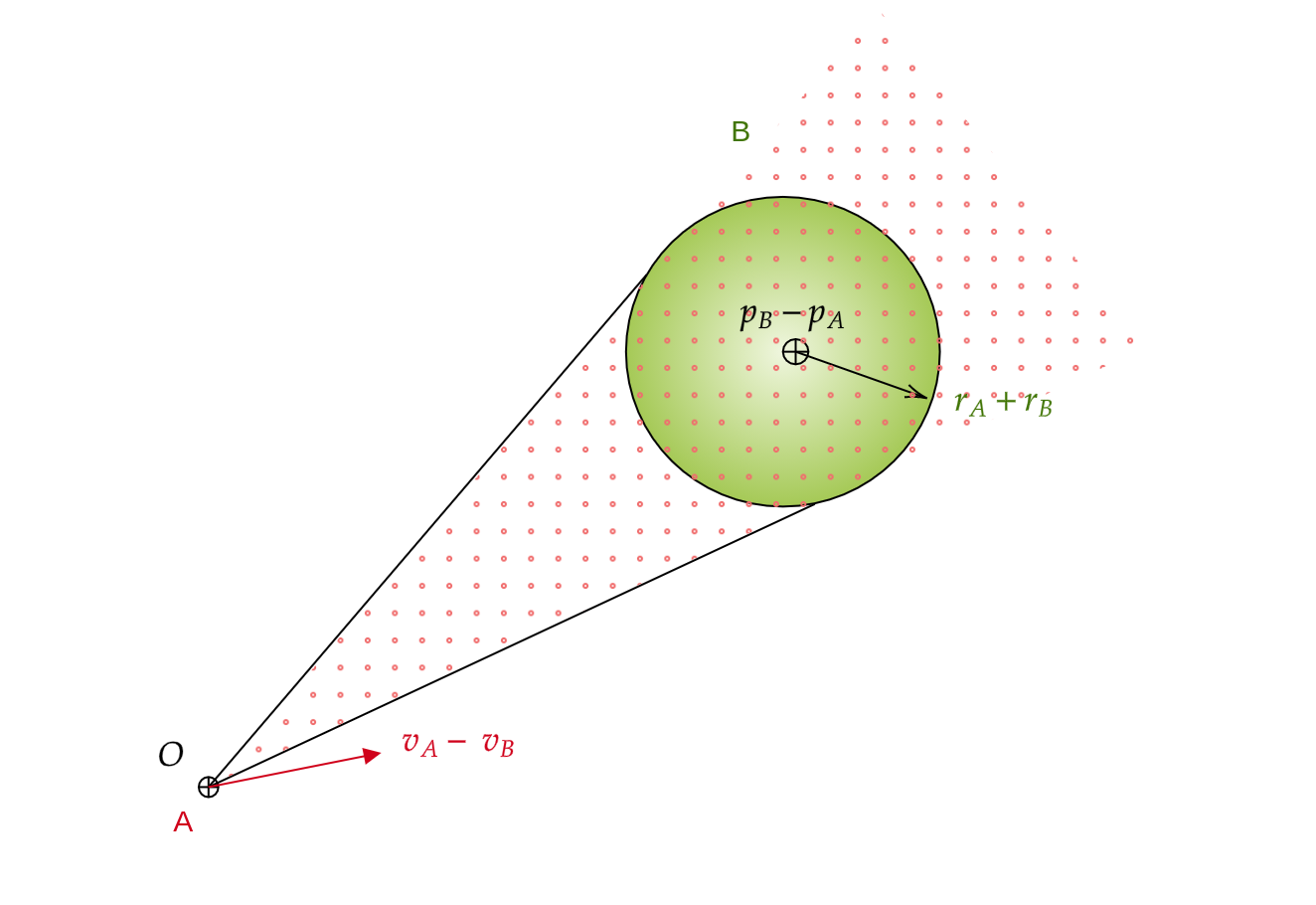Figure 2: Modified scene with red dotted region being the Velocity Obstacle of A induced by B is a cone with apex at A. The relative velocity $v_A - v_B$ does not lead to collision in this scene since it is out of the cone
Now that we have set up the scene let’s go to the definition. The $VO_{A|B}$ (read as Velocity Obstacle of A induced by B) is the set of all relative velocities $\mathbf{v_{AB}}$ that start at A and intersect the disc $\mathcal{D}(p_{BA}, r_{A} + r_{B})$ centered at $p_{BA}$ with the inflated radius. That is,
\[VO_{A|B} = \{ \mathbf{v_{AB}} | \mathbf{v_{AB}}*t \in \mathcal{D}(p_{BA}, r_{A} + r_{B}); \ \ \forall \mathbf{v_{AB}} \in V_{AB}, t \in [0, \inf) \}\]If the relative velocity $v_{AB}$ falls under $VO_{A|B}$ then the robots will collide at some point of time $t \in [0, \inf)$. In the above figure, the velocity obstacle cone is the red dotted region.
The above calculations yield the velocity obstacle for any time, essentially including velocities that will collide so far in the future. Imagine two robots traveling almost parallel to each other but will collide after an hour lol. The current implementation will include those velocities under the VO. We don’t want that! We just want critical velocities that will lead to collision momentarily. Therefore, we define a parameter called time horizon ( $\tau$ ) and consider the relative velocities that will lead to collision before that point in time. This can be achieved as follows:
\[VO^{\tau}_{A|B} = \{ \mathbf{v_{AB}} | \mathbf{v_{AB}}*t \in \mathcal{D}(p_{BA}, r_{A} + r_{B}); \ \ \forall \mathbf{v_{AB}} \in V_{AB}, t \in [0, \tau] \} \\\]Doing this will lead to the change of the range of velocities:
\[\begin{aligned} \mathbf{v}*t &\in \mathcal{D}(p_{BA}, r_{A} + r_{B}) \\ \mathbf{v} &\in \frac{\mathcal{D}(p_{BA}, r_{A} + r_{B})}{t} \end{aligned}\]The range of relative velocities will now be $\mathbf{v} \in \big[\frac{\mathcal{D}(p_{BA}, r_{A} + r_{B})}{\tau}, \text{inf} \big) $. This means that the VO cone will become a fillet cone like in Figure 3:
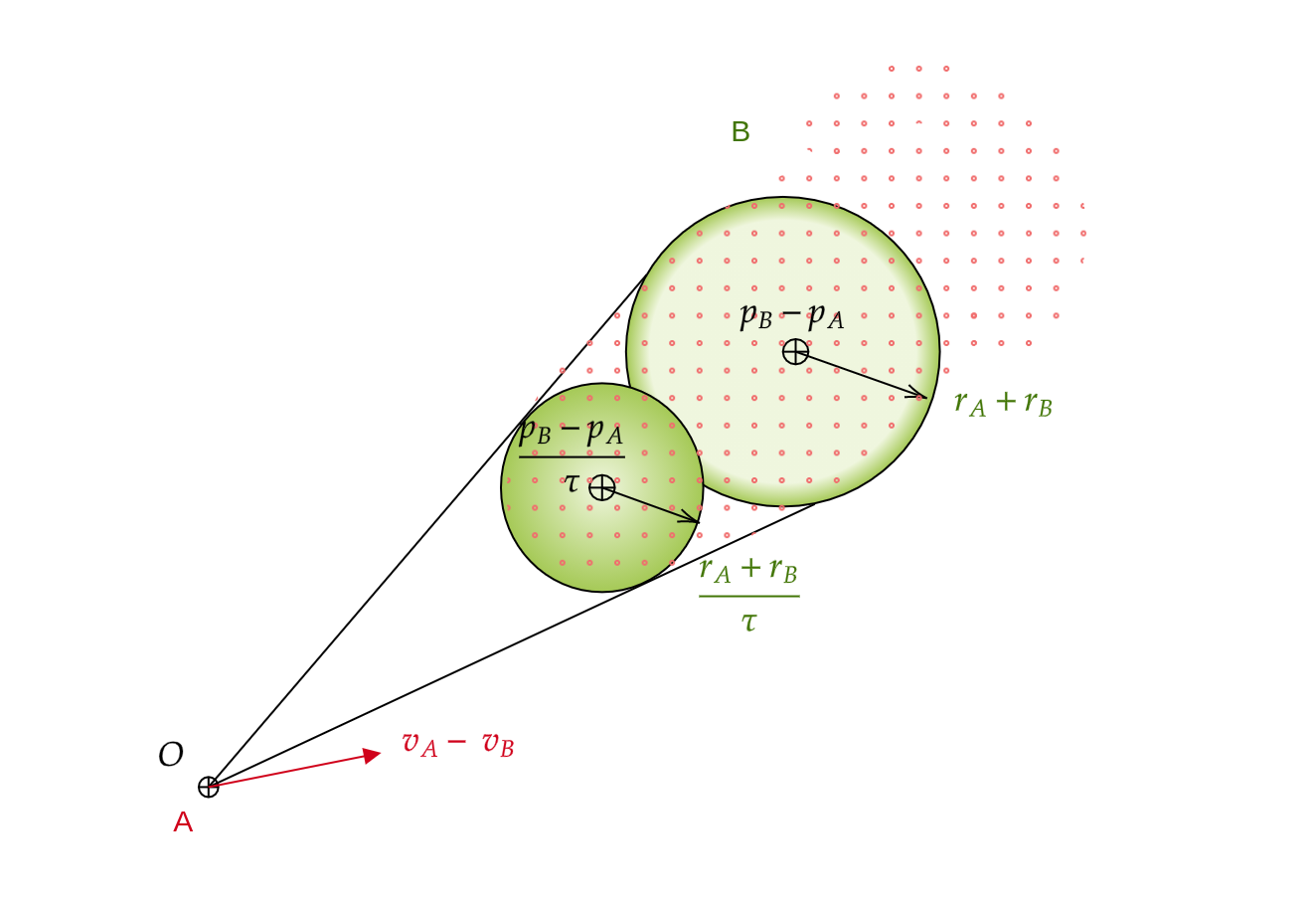Figure 3: Velocity Obstacle of A induced by B within a time horizon is a fillet cone with apex at A
So far we have seen only calculated the set of relative velocities that will lead to collision. But since we are interested in the actual velocity of robot A, we can just add the velocity set of B to the VO set, so if
\[\mathbf{v_{A}} \in VO^{\tau}_{A|B} \oplus V_{B}\]then $\mathbf{v_A}$ will lead to collision. Here $\oplus$ is the Minkowski addition of two sets. The geometrical representation can be seen below:
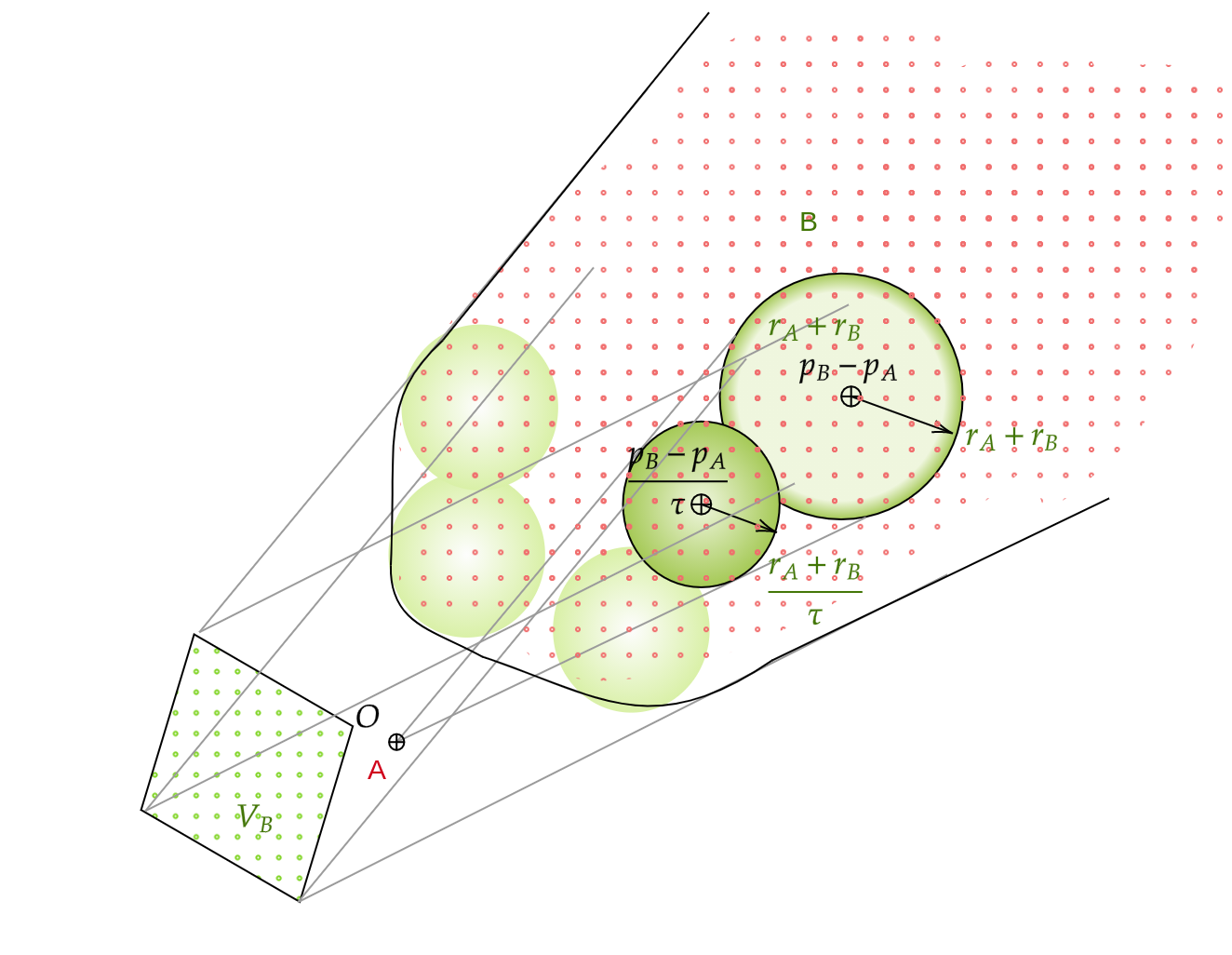Figure 3: The extended Velocity Obstacle of A given that robot B chooses its velocities from the rhombus set $V_B$
Okay now why do we do all this you ask? Well if we know the set of all velocities that lead to collision, we can just avoid these velocities and choose a velocity outside this set! Essentially to avoid collision: $\mathbf{v_A} \notin VO^{\tau}_{A|B} \oplus V_B$ . Simple right? :)
But now we have a LOT of collision avoiding velocities on our hands. How do we know which ones to choose? Stay tuned for part 2 of this post where I talk about Reciprocal Velocity Obstacle (RVO) and its advanced variants. Till then ciao.
