On the cover: Swarm demo scene from Blackmirror: Hated in the Nation
Have you seen the horrifying episode of Black Mirror: Hated in the Nation (trailer)? You know, the one with an artificial bee swarm meant originally for pollination, but someone hacks it and the swarm starts killing 3 most hated people by the end of each day? Setting aside the dystopian future, it’s quite amazing how the artificial bee swarm works to solve a mission (killing people in this case). Quite recently, the company I work for, signed a $15 million contract for 100 drones with the Indian army. This agreement was made under emergency procurement powers given to the army last year, when the India-China standoff in eastern Ladakh began. The drone swarms will be used for foraging, reconnaisance, surveillance and coordinated attacks. All this is possible because of inter drone collision avoidance.
And the best part is, you already know the basics of commonly used collision avoidance algorithms, ie., Velocity Obstacle from the part 1 of this post ;)
The Velocity Obstacle ($VO$) for a robot A induced by robot B augemented by velocity set of B in the environment is given by $VO_{A|B}^{\tau} \oplus V_B$ ie., ( $\oplus$ being the Minkowski sum; refer to part 1 for more details). To avoid collision, robot A can pick a velocity that doesn’t belong to the above set: ie., $\mathbf{v_A} \notin VO_{A|B}^{\tau} \oplus V_B$ . But hold on, robot B also thinks the same right now. It will try to pick a velocity that’s outside $VO_{B|A}^{\tau} \oplus V_A$ ie., the Velocity Obstacle of B induced by A augmented by the velocity set of A.
When the robots are about to collide, the two robots will choose new velocities outside their collision cone and achieve their new velocities. But now with the new collision cones, their old velocities become valid and they are on the collision course again. This conflict resolution at every time step resulting in new conflict, happens until the point of collision. Pretty ironic huh :/ If it’s a static obstacle, this vanilla $VO$ approach works just fine. But it fails when there are moving obstacles adopting the same approach. So vanilla $VO$ robots assume that their obstacles are static or moving with a constant velocity.
Figure 1: Robots A and B trying to avoid collision using their respective VOs
RVO (paper)
The concept of Reciprocal Velocity Obstacle (RVO) was introduced to address the very issue above. The RVO collision cone is constructed as the original cone augmented by the average of the velocities of the agents A and B, ie., $VO_{A|B}^{\tau} \oplus \frac{v_A + v_B}{2}$ . This avoids the ironic collision of vanilla Velocity Obstacle. But there are configurations in which the agents can choose the velocities on the opposite side of their respective collision cones, leading to an oscillating behavior. This oscillation is distinct from the vanilla case and is also known as the reciprocal dance.
Figure 2: Reciprocal dance of two robots UwU
HRVO (paper)
In Hybrid Reciprocal Collision avoidance (HRVO), a directional bias is introduced to each agent in order to eliminate the reciprocal dance. The HRVO cone is the intersection of the leading edge of $RVO$ cone and the trailing edge of $VO$ cone.In practice, HRVO produces smooth trajectories, but there is no theoretical guarantee that it will always avoid the oscillations/collisions.
In the figure 3 below, we can see that the if the apex of the original collision cone is shifted by $v_B$ then it’s the vanilla VO case. If it is shifted by $\frac{v_A + v_B}{2}$ then it’s the RVO case. HRVO shifts the cone by $v_{HRVO}$ which is the intersection of the leading edge of RVO and the trailing edge of VO.
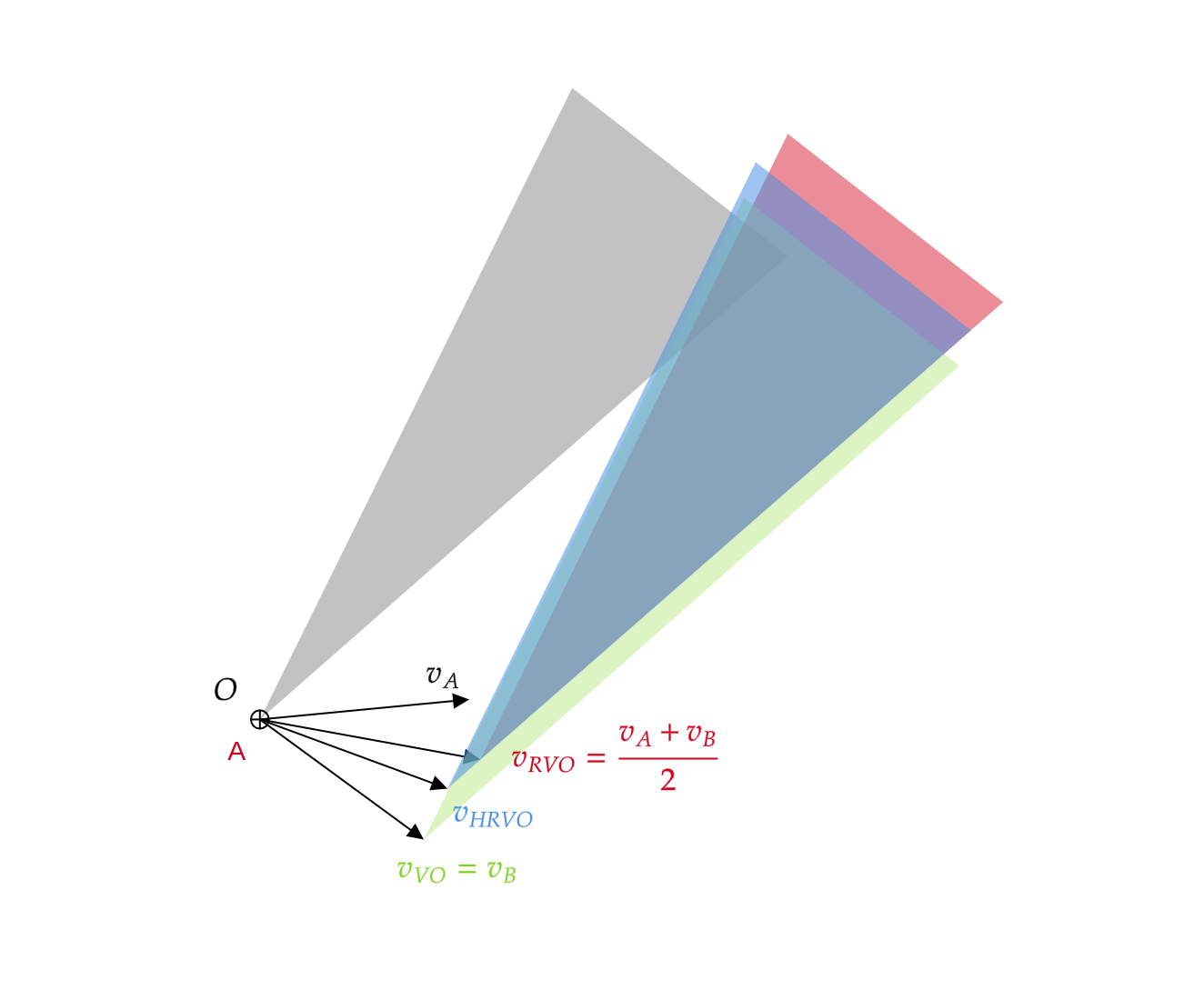Figure 3: Comparison of VO, RVO and HRVO collision cones
ORCA (paper)
Next comes the approach that has been adopted widely these days: Optimal Reciprocal Collision Avoidace (ORCA). This approach contains the time horizon parameter $\tau$ that we defined in the [part 1][part1] of this post. It essentially constructs valid velocity half planes for each agent from which the agent can choose. The half planes are constructed as follows:
We first build a collision cone for agent A (time horizon gives a blunt apex) as mentioned in the part 1. Then we spot the relative preferred velocity of agent A $v_A^{pref} - v_B^{pref}$ . We can see that it’s inside the collision cone. We then find the correction vector $u$ given by the intersection of the normal from the relative preferred velocity to the collision cone. This correction is shared between the agents. That is, agent A gets $v_A^{pref} + \frac{u}{2}$ and agent B gets $v_B^{pref} - \frac{u}{2}$ . The ORCA half planes are perpendicular to the correction normal as shown in figure 4.
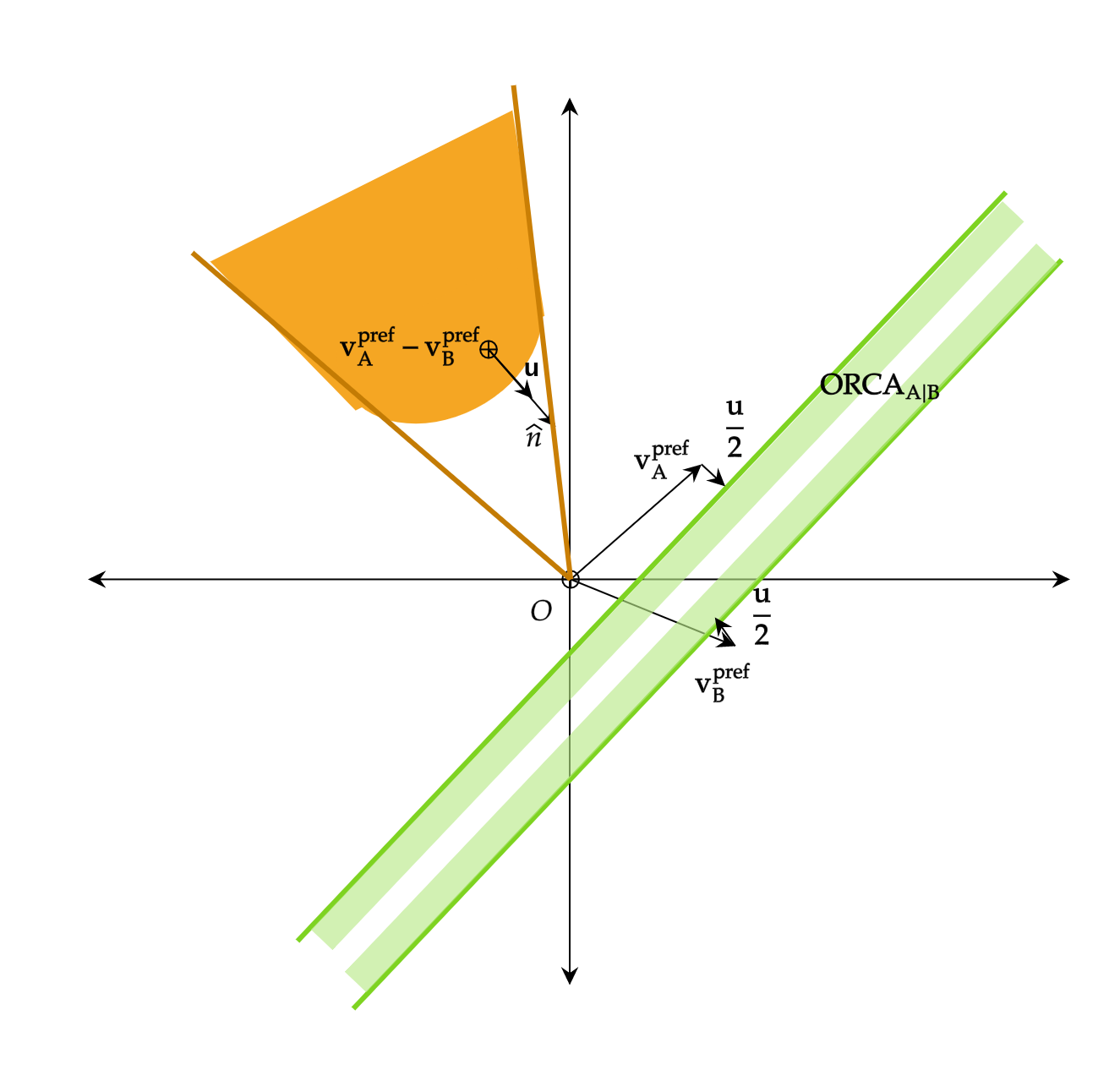Figure 4: ORCA half planes depicted with preferred veelocities of agents A and B
Velocity choosing
Let’s say all our drones are on a mission to kill the top ranked #DeathTo person, like in the Black Mirror episode (sorry I couldn’t ignore the obvious example), they have a goal point to reach. So we employ a path planning algorithm such as VGA or Dijkstra that yields a preferred velocity for all our robots. So we can choose a velocity that belongs to the collision avoiding set while being close to the preferred velocity.
This is exactly what is being done for ORCA as shown before. In the case of multiple agents in the environment, ORCA yields multiple half planes that will tell us whether collision free trajectory is possible. Also the preferred velocities are not always available if central communication doesn’t exist. In that case, the preferred velocities are set to the current velocities which give an idea of the agent’s preference.
I made a small working demo in Unity consisting of 10 agents in a 2D plane with the following ORCA parameters:
- agent radius: 5 m
- neighbour distance: 50 m
- time horizon: 50 s
The goal for each agent is to start from their current position and move to their respective negative coordinates say from $(10,20)$ to $(-10,-20)$ and this is how it looks! Pretty nifty huh :)
Figure 5: ORCA demo with 10 agents avoiding collision while navigating to their goal points
So now you’re fully equiped to launch your own drone swarm with collision avoidance. Just add Augmented Reality and you’re on your way to become the next Mysterio. Until next time.
