Human Blood is composed of blood cells (also called corpuscles) suspended in blood plasma. Study of human blood and its flow in blood vessels is crucial for diagnosis, pathology and design of biomedical devices. Study of deformative properties and flow of RBCs and cancer cells in minute vessels have peaked the interest of biologists and pathologists, since affected cells differ in their behavior compared to the healthy cells. In this thesis, we use FORTRAN codes to model the RBCs in micro flow domain. We use Velocity Verlet algorithm for time integration.
Boundary Conditions: Generally multiple layers of frozen particles at same particle density as that of the fluid are used to simulate the stationary wall. But since this is computationally expensive, we use modified Instantaneous Frozen Particle (IFP) model as the boundary condition to model the walls. Drawback: It sets of pressure waves which cause density fluctuations in the domain of a larger magnitude than the other methods.
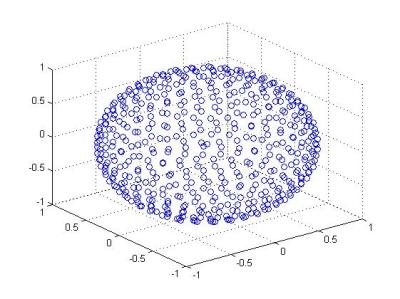500 equidistant points are chosen inside a sphere to model a cancer cell/RPIFP particle
To circumvent this problem, we use a modified version of IFP. We call this Random Position Instantaneous Frozen Particle (RPIFP) Method. In IFP, as the force between each particle and the boundary is directed towards the center, the density fluctuations appear much more significant. RFIFP attempts to avoid this by introducing a small random component to the position of the boundary particle. In addition to this, adaptive boundary conditions control density fluctuation near the boundary.
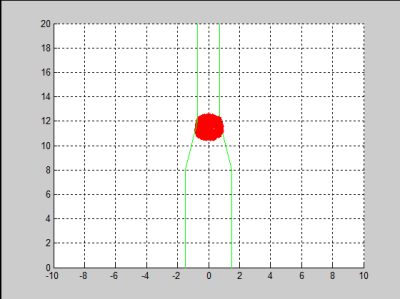Mesoparticle squeezing through the contricted neck
Low Torus Ring Structure: RBC in this simulation is modelled as a ring of 10 colloidal particles connected by worm-like chains. This model is adopted since simulating the original spectrin network (cytoskeleton) of an RBC is computationally quite expensive. This model is also useful for simulating a large number of RBCs in the domain.
| 
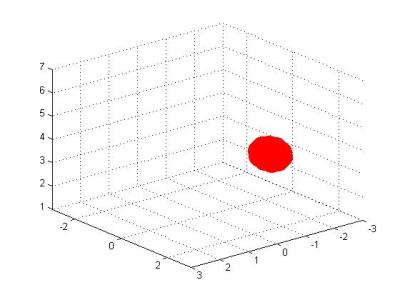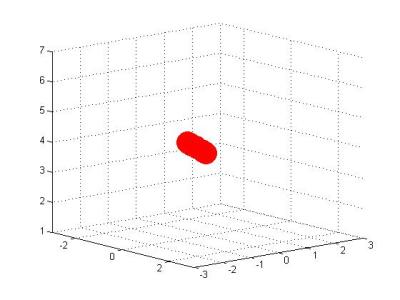Low torus ring structure of RBCs travelling through a cylindrical constriction toppling and turning as they travel in the domain